19+ vector spherical harmonics
The mcx calculator can make these rotation matrices for you. The vector spherical harmonic analysis of eqs 1 4 forms the basis of several useful Galerkin methods for solving a range of problems in spherical geometries.
Spherical Harmonics
19 vector spherical harmonics Senin 24 Oktober 2022 TR 11-12 Virtual or TR 12-1 Virtual or TR 3-4 Virtual or TR 4-5 Virtual Introduces classical mechanics.

. Vector spherical harmonics on mathbbS2subset mathbbR3 have wide applications in geophysics quantum mechanics and astrophysics. The vector spherical harmonic expansion technique that has been developed as part of my PhD research on modeling of. There is not complete uniformity in the definition of the vector spherical harmonics so it is possible that different definitions may actually refer to.
SPHERICAL HARMONICS Therefore the eigenfunctions of the Laplacian on S1 are the restrictions of the harmonic polynomials on R 2to S 1and we have a Hilbert sum. If ℓ 0 then Yℓ1 jℓ1mθφ is the only surviving vector spherical harmonic. In the representation of a tangent field one.
Vector Spherical Harmonics E1 Spherical Harmonics E11 Legendre Polynomials The Legendre polynomials are solutions to Legendres di erential equation d dx 1 x2 d dx P lx P lx 0. The components of the VSH are complex-valued. In mathematics vector spherical harmonics VSH are an extension of the scalar spherical harmonics for the use with vector fields.
The and are related as follows using standard conventions 2 as in eg. It is instructive to work in a. Vectors in vector spherical harmonics then the angular dependence will cancel out.
NRD is distributed as. In the present case Therefore 73-5 Since the possible values of J are l 1 l l 1 73-6. 3 Vector harmonics The.
Let r θ φ be spherical. A spectrally accurate numerical method for computing the sphericalvector spherical harmonic expansion of a functionvector field with given elemental nodal values on a spherical surface. Vector Spherical Harmonic The spherical harmonics can be generalized to vector spherical harmonics by looking for a scalar function and a constant vector such that 1 2 3.
In mathematics vector spherical harmonicsVSH are an extension of the scalar spherical harmonicsfor use with vector fields. Where The inverse operation is. 19 Spherical vector wave expansion functions are computed from.
From 15-54 with M m1 m2. Towards this end one can readily confirm the relations among scalar and vector spherical harmonics. Definition Several conventions have been used to.
In systems with spin it is more convenient in many cases to define a total rotation. We shall now express in terms of vector spherical harmonics. Vector Spherical Harmonics and Multipoles.
There are 19 vector spherical harmonics-related words in total not very many I know with the top 5 most semantically related being spherical coordinate system unit vector mathematics. 1238 This is an orbital rotation operator. Spherical coordinate representation described above Yk mxb with the coordinate transformation law xbxa to obtain Yk mxb Yk mxaxb.
The other two vector spherical harmonics can be written out in a similar fashion.
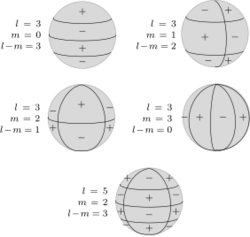
Physics Spherical Harmonics Handwiki

C8m5ld8ilj8c2m

Table Of Spherical Harmonics Wikipedia

Table Of Spherical Harmonics Wikipedia

Vector Spherical Harmonics Wikipedia
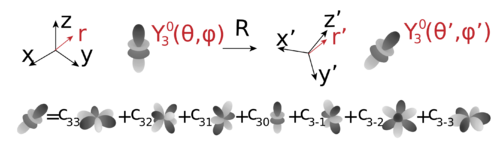
Physics Spherical Harmonics Handwiki

Vector Spherical Harmonics 1 Introduction

Spherical Harmonic Basis Of Selective Degree And Orders Download Scientific Diagram
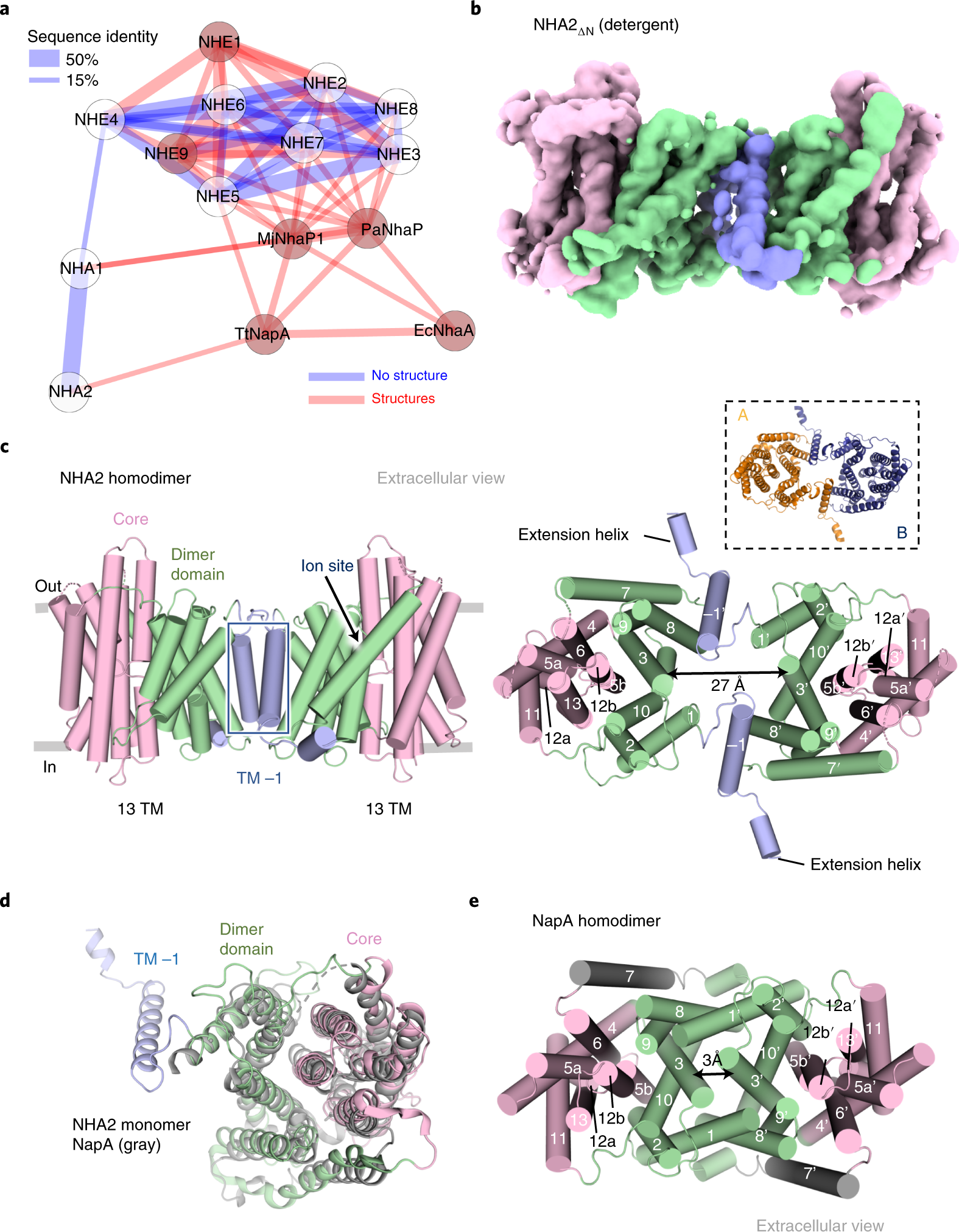
Structure Mechanism And Lipid Mediated Remodeling Of The Mammalian Na H Exchanger Nha2 Nature Structural Molecular Biology
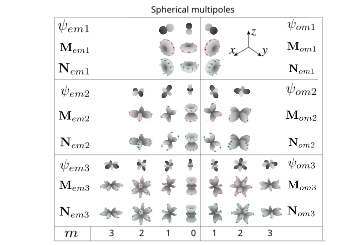
Vector Spherical Harmonics Wikipedia

Spherical Harmonics

Simon S Tech Blog Spherical Harmonic Lighting

Table Of Spherical Harmonics Wikipedia

Vector Spherical Harmonic From Wolfram Mathworld

Spherical Harmonics

Vector Spherical Harmonics

Table Of Spherical Harmonics Wikipedia